Transmissão de Sinais

Sinais:

São muitos os sinais que ocorrem no nosso quotidiano. As formas de comunicação envolvem o uso de sinais. Uma característica que permite detectar sinais à nossa volta é a sua possibilidade de perturbar.

Um sinal é uma perturbação de qualquer espécie que é usada para comunicar (transmitir) uma mensagem ou parte dela.

Em termos formais, um sinal é uma função que veicula informação acerca de um determinado fenómeno físico:

. Quando a função depende apenas de uma variável, diz-se que o sinal é unidimensional. É o caso da fala;

. Quando a função depende de duas ou mais variáveis, diz-se que o sinal é multidimensional.

Uma maneira de proceder à identificação de diferentes tipos de sinais baseia-se como o sinal se localiza no espaço e no tempo:

. A localização no tempo está relacionada com o instante em que a perturbação foi produzida.

. A localização no espaço etá relacionada com o local onde foi produzida a perturbação.

Tipos de sinais:

. Contínuo: se for definido para qualquer valor da variável tempo.

. Curta duração: quando se define somente em intervalos de tempo curtos e em instantes isolados. Estes sinais designam-se por pulsos (ou impulsos).

. Periódico: é repetido ao fim de intervalos de tempo iguais.

. Aperiódico: repete-se mas em intervalos de tempo diferentes.

 

Propagação de um Sinal: energia e velocidade de propagação (modelo ondulatório).

À nossa volta detectam-se sinais que, após serem emitidos, se propagam, percorrendo certas distâncias. Por exemplo, a propagação de um sinal sonoro, de um sinal luminoso e de um sinal electromagnético.

 

Tipos de Ondas:

Os sinais podem originar ondas que se propagam no espaço e no tempo.

Tipos de ondas quanto ao meio:

. Agumas exigem um suporte material físico elástico para se propagarem - são as ondas mecânicas (sinais sonoros).

. Outras não necessitam de suporte material para se propagarem - é o caso das ondas electromagnéticas (sinais luminosos).

Os sinais sonoros e os sinais electromagnéticos propagam-se no espaço e no tempo por meio de movimentos ondulatórios.

Tipos de ondas quanto ao modo de propagação:

. Onda transversal - os pontos da mola oscilam perpendicularmente na direcção em que a onda se propaga (ex: sinais electromagnéticos).

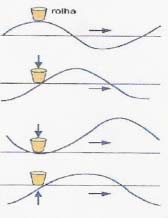
. Onda longitudinal - as partículas do meio oscilam na direcção em que a onda se propaga (ex: sinais sonoros).

Uma onda que se propaga na água é um exemplo comum de um movimento ondulatório. Admite-se a existência de forças de tensão superficial na superfície livre do líquido que, por isso, se comporta como um meio elástico. Qualquer perturbação que ocorra neste meio, provoca uma deformação, a qual se propaga sob a forma de círculos, formando ondas.

 

Um fenómeno ondulatório caracteriza-se pela existência de uma perturbação inicial que altera localmente uma propriedade física do meio e pela propagação dessa perturbação através do meio.

A água no seu conjunto não flui - não há mivimento radial da água. É a perturbação que se movimenta e se propaga. A água é o meio que permite a transmissão da perturbação de um ponto para outro da superfície. A perturbação também transfere energia para a rolha, mas não ocorre transferência de matéria.

Pode determinar-se o valor da velocidade de propagação do movimento ondulatório na água. Para isso, considera-se um ponto da superfície e observam-se as ondas que passam nessa posição. Consegue-se avaliar o espaço percorrido, por exemplo, por uma crista de onda e o intervalo de tempo entre a chegada a essa posição de duas cristas consecutivas.

A velocidade de propagação depende das propriedades físicas do meio e não depende da quantidade de energia transferida inicialmente. O som propaga-se com velocidades diferentes em meios diferentes

 

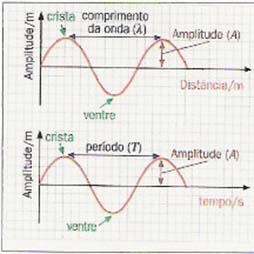
Um caso particular: a onda sinusoidal

. Quando uma onda resulta da emissão de um sinal repetido a intervalor regulares, independentemente da sua forma, diz-se que estamos perante uma onda periódica.

. À medida que uma onda periódica se propaga, cada ponto do meio oscila, regularmente, com o mesmo período e a mesma frequência do sinal que a origina.

Uma onda periódica tem uma periodicidade no tempo e no espaço. A periodicidade no tempo de uma onda periódica associa-se ao seu comprimento de onda.

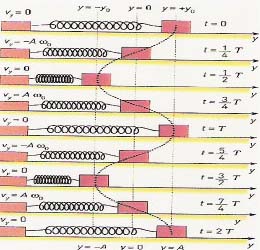
Movimento harmónico simples

O deslocamento do corpo que oscila pode ser descrito em função do tempo. Como o movimento é periódico, é de esperar que as leis do movimento sejam experssas por funções igualmente periódicas.

 

Oscilação harmónica

A curva a tracejado é o gráfico y = f (t) correspondente às diferentes posições do corpo, em função do tempo, num movimento harmónico simples.

O afastamento em relação à posição de equilíbrio, a que se chama elongação, em cada instante, pode ser descrito pela função y = f (t).

y = A sin (v t)

 

Sinal harmónico e onda harmónica

As propriedades especiais dos sinais harmónicos fazem deles um exemplo importante de sinais áudio. Os engenheiros electrotécnicos e de som investigam o que acontece com este tipo de sinais quando pretendem eliminar ruídos na aparelhagem electrónica utilizada em programas sonoros.

A função que descreve os sinais harmónicos é trigonométrica. Varia periodicamente no tempo.

Os sinais harmónicos são sinusoidais e periódicos.

Todos os sinais harmónicos têm uma origem comum. Resultam de perturbações produzidas por osciladores animados de movimento harmónico simples. Um oscilador descreve um movimento harmónico simples, num dado referencial, quando a sua coordenada de posição nesse referencial é uma função sinusoidal num dado intervalo de tempo.

Um sinal harmónico, com um dado período e uma certa frequência, pode propagar-se no espaço e no tempo através de uma onda harmónica. Há muitos tipos de ondas harmónicas. Mas todas as ondas harmónicas têm uma origem comum: um sinal harmónico proveniente de um oscilador. Isto quer dizer que as ondas harmónicas resultam de perturbações periódicas produzidas por um movimento harmónico simples.

 

A - amplitude das oscilações;

y - elongação do corpo oscilante. O seu valor máximo coincide com A e o mínimo com -A.

As funções trigonométricas seno e coseno são chamadas funções harmónicas.Por isso, os movimentos descritos pela lei y = A sin (v t) são chamados harmónicos.

 

Outros Trabalhos Relacionados