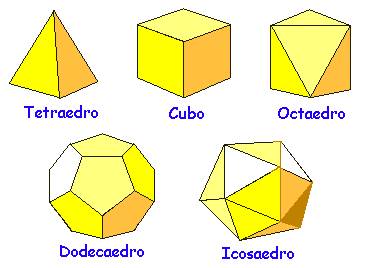
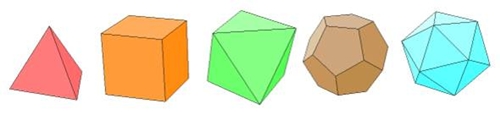
|
Os sólidos platónicos são sólidos convexos cujas arestas formam polígonos planos regulares congruentes. A sua designação deve-se a Platão, que os descobriu em cerca de 400 a.C.. A existência destes sólidos já era conhecida pelos pitagóricos, e os egípcios utilizaram alguns deles na arquitectura e noutros objectos que construíram. Existem apenas cinco sólidos platónicos, que são os seguintes:
Estes sólidos foram adquirindo ao longo dos tempos diversos significados místicos. Por exemplo, Kepler sentia uma grande admiração e reverência por eles (Porquê apenas cinco?) e chegou mesmo a tentar explicar os movimentos planetários a partir deles. Além disso, interpretou, no Harmonices Mundi, as associações de Platão da seguinte forma:
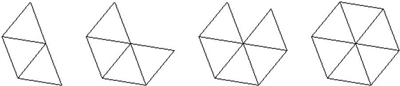
Uma demonstração de que são apenas cinco os sólidos platónicos pode ser obtida através do processo da sua construção, como Platão fez num seu texto incluído no diálogo Timeu. Para a construção dos sólidos platónicos, por definição, apenas podemos utilizar polígonos regulares congruentes. Comecemos por considerar o triângulo equilátero, que é o polígono regular com menos lados. Quantos poliedros, cujas faces são apenas este polígono, conseguimos construir? Para responder a esta pergunta, centremos a nossa atenção nos vértices dos possíveis poliedros (basta considerar apenas um, pois os restantes são idênticos). Com dois triângulos equiláteros, não se consegue constituir um vértice de um poliedro, pois um ângulo sólido tem que ser constituído pelo menos por três planos. Com três triângulos equiláteros é possível constituir um vértice de um poliedro, que é concretamente o tetraedro. Esta possibilidade prende-se com facto de a soma das amplitudes dos ângulos internos dos diversos triângulos adjantes, no vértice, ser inferior a 360º, exactamente 180º. Se considerarmos quatro triângulos equiláteros, cuja soma das amplitudes dos ângulos internos adjantes no vértice é de 240º, obtemos o octaedro. Considerando cinco desses triângulos num vértice, essa soma é de 300º, ainda inferior a 360º, e obtemos o icosaedro. Passando para seis triângulos equiláteros, chegamos a uma impossibilidade. A soma das amplitudes dos ângulos internos adjantes no vértice é, neste caso, 360º, o que não permite "fechar" o vértice, isto é, formar um ângulo sólido, pois os triângulos ficam todos sobre o mesmo plano (formando uma pavimentação do plano em torno do suposto vértice). A consideração de um número maior de triângulos equiláteros em torno de um vértice, obviamente já não possibilita a construção de um poliedro.
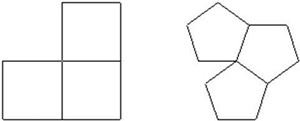
O pressuposto de construção que tem estado a ser utilizado é o de que a formação de um ângulo sólido no vértice de um poliedro só é possível se a soma das amplitudes dos ângulos internos dos polígonos adjacentes no vértce for inferior a 360º. Considerando o quadrado, e o pressuposto atrás enunciado, chegamos à conclusão de que apenas conseguimos construir o cubo. Com pentágonos, apenas conseguimos construir o dodecaedro.
Com hexágonos não se consegue construir nenhum sólido platónico. Basta verificar que três hexágonos adjacente em torno de um ponto (supostamente um vértice) pavimentam o plano, pois a soma das amplitudes dos ângulos internos desses hexágonos é precisamente 360º, o que não permite formar um ângulo sólido. Um número maior de hexágonos, obviamente, que também não permite a construção de um sólido platónico. Analogamente, com polígonos com um número maior de lados isso também não é possível.
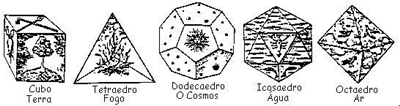
Enumeremos então os sólidos que acabámos de construir: tetraedro, octaedro, icosaedro, cubo e dodecaedro. São precisamente cinco, como se queria demonstrar. Outra forma demonstrar a existência de apenas cinco sólidos platónicos é através da fórmula de Euler, considerando as restrições relativas aos vértices, arestas e faces inerentes aos sólidos platónicos. Um pouco de História: Grandes filósofos e matemáticos dedicaram a vida ao estudo da geometria. Enquanto a escola pitagórica, por exemplo, tinha como lema "Tudo são números" a escola de Platão (a Academia) tinha escrito sobre a porta, "Não entre aqui ninguém que não seja geométra". Platão foi o primeiro matemático a demonstrar que existem apenas cinco poliedros regulares: o cubo, o tetraedro o octaedro, o dodecaedro e o icosaedro. A eles se referiu no seu dialogo "Timeu" pelo que esses cinco poliedros regulares passaram a ser designados por sólidos platónicos. O conhecimento destes sólidos parece ter sido desencadeado num encontro com Arquitas que, em viagem à Cecília, no sul de Itália, encontraria Platão. Para este, o Universo era formado por um corpo e uma alma, ou inteligência. Na matéria havia porções limitadas por triângulos ou quadrados, formando-se elementos que diferiam entre si pela natureza da forma das suas superfícies periféricas. I. Se fossem quadradas, teríamos
o cubo - elemento terra. II. Se fossem triângulos equiláteros, teríamos
o tetraedro - o elemento fogo.
o octaedro - o elemento ar.
o icosaedro - o elemento água. III. Se fossem pentágonos, teríamos
o dodecaedro - simbolizava o Universo. Embora chamados Platónicos, Proclus atribuiu a construção destes poliedros a Pitágoras, supondo-se que é também a ele que se deve o teorema: Há somente cinco poliedros regulares. Hoje sabe-se que o teorema só é verdadeiro para os poliedros regulares convexos. Alguns séculos mais tarde, em 1597 Kepler, inspira-se nos poliedros regulares para estudar o movimento dos seis planetas até então conhecidos (Saturno, Júpiter, Marte, Terra, Vénus e Mercúrio) e publica a sua obra "The Cosmographic Mystery", onde utiliza um modelo do sistema solar composto por esferas concêntricas, separadas umas das outras por um cubo, um tetraedro, um dodecaedro, um octaedro e um icosaedro para explicar as distâncias relativas dos planetas ao sol.
É também Kepler, que vai descobrir o primeiro poliedro regular côncavo, que é o dodecaedro estrelado, de faces regulares que resulta do prolongamento das faces do dodecaedro.
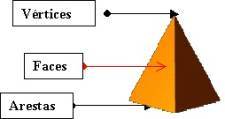
No séc. XVIII, Louis Poinsot descobriu três novos poliedros regulares não convexos. Há nove poliedros regulares e Cauchy provou que não existem mais. Apresentação dos sólidos platónicos: Poliedros (poli = muitos; hedros = faces) são sólidos delimitados por regiões planas (polígonos) que constituem as denominadas faces. Os segmentos de recta que limitam as faces designam-se por arestas e os pontos de encontro destas por vértices.
Um poliedro diz-se convexo quando os ângulos diedros formados por duas faces consecutivas forem menores que 180º. Sólidos Platónicos são poliedros convexos cujas faces são polígonos regulares (polígonos com os lados e ângulos todos iguais) e que têm o mesmo número de faces que se encontram em cada vértice.
Se considerarmos um qualquer sólido platónico e "unirmos" os pontos centrais de faces adjacentes, obtemos um novo sólido platónico. Estes dizem-se duais um do outro.
Será que todos os poliedros regulares são convexos? Kepler descobriu dois poliedros que são simultaneamente regulares e não convexos- o pequeno dodecaedro estrelado e o grande dodecaedro estrelado. Mais tarde, foi provado que existem apenas nove poliedros regulares, sendo cinco convexos (sólidos platónicos) e quatro não convexos (sólidos de Kepler-Poinsot).
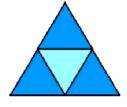
Planificações: Tetraedro: É um poliedro regular com 4 faces sendo estas triângulos equiláteros, 4 vértices e 6 arestas. O Tetraedro pode formar-se a partir de um molde com quatro triângulos.
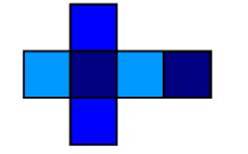
Hexaedro ou Cubo: É um poliedro regular com 6 faces sendo estas quadrados, 8 vértices e 2 arestas. O cubo pode ser formado a partir de um molde com seis quadrados.
Octaedro: É um poliedro regular com 8 faces sendo estas triângulos equiláteros, 6 vértices e 12 arestas. O octaedro pode ser formado a partir de um molde com oito triângulos equiláteros.
Icosaedro: É um poliedro regular com 20 faces que são triângulos equiláteros, 12 vértices e 30 arestas. O icosaedro pode ser formado a partir de um molde de vinte triângulos equiláteros.
Dodecaedro: É um poliedro regular com 12 faces que são pentágonos, 20 vértices e 30 arestas. O dodecaedro pode formar-se a partir de um molde com vinte pentágonos.
Sólidos Platónicos Na geometria e algumas antigas teorias fisícas, um solido platónico é um poliedro convexo com: . Todas as faces são polígonos congruentes . O mesmo número de faces encontra-se em todos os vértices Os cinco sólidos platónicos, são conhecidos desde a antiguidade clássica, e a prova que são os únicos poliedros regulares pode ser encontrada nos Elementos de Euclides. Tabela
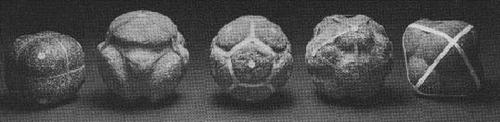
Resumo Os alunos serão guiados a resolver alguns desafios mencionados ao longo do texto. Ao construir poliedros regulares, os alunos irão encontrar a fórmula de Euler, que quando aplicada a um dado poliedro regular convexo se conclui que esse poliedro terá de ser um dos cinco Sólidos Platónicos. Discute-se o aparecimento de poliedros em estruturas moleculares da Biologia/Química. Finalmente introduz-se a noção de simetria e calcula-se o grupo das simetrias do tetraedro. Dado o uso de animações estas notas devem ser lidas usando a ligação via internet da página do encontro. Conteúdo 1. Introdução 2. Construção dos Sólidos Platónicos e a fórmula de Euler 3. Classificação dos Poliedros regulares 4. Simetrias 5. Bibliografia 1 Introdução Os poliedros são estudados desde a Grécia Antiga na escola de Pitágoras, 600 aC, embora haja evidencia de que os Povos Neolíticos que viveram na Escócia tinham esculpidos alguns destes sólidos 1000 anos antes. Alguns destes modelos, ver figura 1, encontram-se no Museu Ashmolean em Oxford, Reino Unido.
FIG 1: Modelos Neolíticos dos Sólidos Platónicos Os poliedros ilustrados na figura 2 tiveram um papel crucial na Filosofia de Platão, que serão os nossos objectos de estudo.
FIG 2: Tetraedro Cubo (Hexaedro) Octaedro Dodecaedro Icosaedro Na sua admiração e entusiasmo (porquê só cinco?) pela Geometria, Euclides e a Grécia Antiga, chamou a estes os Sólidos Platónicos associando-os aos átomos do universo. Da mesma forma que hoje nós acreditamos que toda a matéria é feita de combinações de átomos, também na Grécia Antiga se acreditava que a matéria era feita com os sólidos Platónicos. Também se acreditava que toda a matéria também tinha o lado místico. Assim, no diálogo Timaios, Platão associou o tetraedro ao elemento fogo, o cubo à terra, o icosaedro à água e finalmente o dodecaedro ao quinto elemento (o universo).
Pitágoras (569? aC—475 aC) Platão (427 aC—347 aC) Euclides (325 aC—265 aC) O cubo, tetraedro e o dodecaedro tinham sido considerados pelos pitagóricos, e os restantes por Theætetus – amigo de Platão -- que pensava que o universo estava envolvido por um dodecaedro gigante. Os pitagóricos sabiam que existiam apenas cinco regular sólidos regulares convexos e que cada um podia ser rigorosamente circunscrito por uma esfera. Euclides descreve estes sólidos no seu livro Elementos, parte XIII, da proposição 13 à proposição 17, onde se encontra o argumento heurístico de que estes são os únicos sólidos regulares. O matemático Euler fez a demonstração deste resultado no séc. XVIII. Kepler no início do séc. XVII, sugeriu associar os Sólidos Platónico aos planetas conhecidos nessa altura: Mercúrio, Vénus, Marte, Júpiter e Saturno.
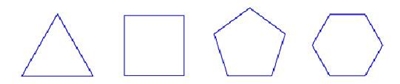
Euler (1707---1783 Kepler (1571---1630) 2 Construção dos Sólidos Platónicos e a formula de Euler Para resolver os seguintes desafios, será necessário fazer vários recortes dos seguintes polígonos:
FIG 3: Triângulo Equilátero Quadrado Pentágono Regular Hexágono Regular Desafio 1: a) Cole três triângulos com um vértice comum. A partir daqui construa um sólido com o mesmo tipo de vértice. Qual foi o sólido que obteve? b) Repita o processo descrito em a) com quatro triângulos à volta do mesmo vértice, depois com cinco, seis, etc. O que está obtem? Desafio 2: ala) Cole três quadrados à volta do mesmo vértice. A partir daqui construa um sólido com o mesmo tipo de vértice. O que obteve? b) Repita este processo com quatro, cinco,... quadrados à volta do mesmo vértice. Qual é a conclusão? Desafio 3: a) Ligue três pentágonos à volta do mesmo vértice. A partir daqui construa um sólido com o mesmo tipo de vértice. O que obteve? b) Repita este processo com quatro, cinco,... pentágonos à volta do mesmo vértice. Qual é a conclusão? Desafio 4: a) Cole três hexágonos à volta do mesmo vértice. A partir daqui construa um sólido com o mesmo tipo de vértice. O que obteve? Conseguiu construir um sólido? Obtém-se assim os cinco Sólidos Platónico e facilmente se conclui a seguinte tabela (como exercício, use a planificação destes sólidos para preencher esta tabela).
. Tetraedro (4 vértices, 6 arestas, 4 faces (triângulos equiláteros) . Cubo ou hexaedro (8 vértices, 12 arestas, 6 faces (quadrados) . Octaedro (6 vértices, 12 arestas, 8 faces (triângulos equiláteros) . Dodecaedro (20 vértices, 30 arestas, 12 faces (pentágonos) . Icosaedro (12 vértices, 30 arestas, 20 faces (triângulos equiláteros).
Formula de Euler (facto elementar da moderna topologia algébrica – ramo da Matemática): Seja P um poliedro convexo (não necessariamente regular), então temos:
onde F, A e V, denotam o número total de faces, arestas e vértices (respectivamente) do poliedro. Notamos que a primeira prova desta fórmula foi feita por Cauchy. Desafio 5: Verifique a validade da fórmula de Euler em cada um dos sólidos Platónicos! Ligando os centros de todos as faces adjacentes de cada Sólido Platónico obtém-se assim um outro sólido (mais pequeno) que é novamente um Sólido Platónico. Designa-se por sólido dual a este sólido que se obteve a partir do inicial.
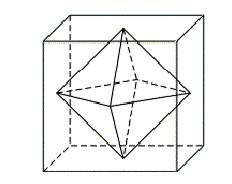
FIG 4: O dual do Cubo é o Octaedro Como exemplo, temos que o Octaedro é o sólido dual do Cubo, como ilustra a figura 4. Como o número de faces (vértices) do sólido dual é por construção igual ao número de vértices (faces) do sólido original, podemos então concluir a validade da última coluna da Tabela preenchida em cima.
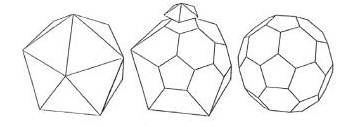
Nota 1 Os Sólidos de Arquimedes ou poliedros semi-regulares são, grosso modo, poliedros convexos cujas faces são polígonos regulares de mais de um tipo. Todos os seus vértices são congruentes, isto é, existe o mesmo arranjo de polígonos em torno de cada vértice. Além disso, todo vértice pode ser transformado em outro vértice por uma simetria do poliedro. Existem apenas treze poliedros arquimedianos e são todos obtidos por operações sobre os Sólidos Platónicos. A título de exemplo, um deles designa-se por Icosaedro truncado e que é usada na moderna bola de futebol: 32 faces, 12 pentágonos, 20 hexágonos:
FIG 7: Construção da bola de futebol a partir do Icosaedro Obtém-se assim a (moderna) bola de futebol:
FIG 8: Icosaedro truncado (ou bola de futebol ou ainda a molécula do futeboleno C60) O Icosaedro truncado reencontrou novas e interessantes aplicações com a descoberta da molécula do futeboleno C60 (buckminsterfullereno ou buckyball) que foi comunicada num artigo da revista Nature, em 1985, por H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl e R. E. Smalley. O primeiro e os dois últimos foram galardoados com o prémio Nobel da Química de 1996. Esta descoberta marca o início de uma nova área do conhecimento: a nanotecnologia. A molécula tem uma estrutura semelhante a uma bola de futebol. É constituída por 60 átomos de carbono, que formam 12 pentágonos e 20 hexágonos. Faz-se notar que se descobriu recentemente que muitos vírus, p.ex. o vírus da herpes, têm a forma de icosaedro! Aliás, a ligação entre a estrutura geométrica dos átomos e alguns sólidos já tinha sido referida pelo próprio Platão, por exemplo: o sal mineral, i.e. cloreto de sódio NaSl, aparece na forma de cristais cúbicos; floreto de cálcio CaF2 na forma de octaedro e a pirite, i.e. Disulfito de Ferro FeS2 na forma de dodecaedros. Os duais dos Sólidos de Arquimedes são designados por Sólidos de Catalan e a fórmula de Euler é válida para os poliedros convexos! Nota 2 Uma vez que todos os poliedros convexos estão classificados é natural perguntar se haverá poliedros convexos que não sejam regulares? Kepler, em 1619, descobriu dois poliedros que são simultaneamente regulares e não convexos: o pequeno dodecaedro estrelado e o grande dodecaedro estrelado. Dois séculos mais tarde provar-se-ia que existem apenas nove poliedros regulares: os cinco sólidos platónicos e quatro poliedros regulares não convexos - os Poliedros de Kepler-Poinsot. Um Poliedro de Kepler-Poinsot é um poliedro regular não convexo. Todas as suas faces são polígonos regulares iguais. E em todos os vértices encontram-se o mesmo número de faces (comparar com Sólidos Platónicos). Existem quatro Poliedros de Kepler-Poinsot:
Desafio 7: A formula de Euler não se verifica para dois deles --- Quais? Assim temos apenas nove poliedros regulares, sendo cinco convexos (sólidos platónicos) e quatro não convexos (sólidos de Kepler-Poinsot). Resumo: (1) Existem exactamente 5 poliedros regulares convexos (os sólidos Platónicos) (2) (2) Existem exactamente 4 poliedros semi-regulares e convexos (sólidos de Arquimedes) (3) (3) Existem exactamente 13 poliedros regulares não convexos (sólidos de Kepler--Poinsot) Platão
Vida Platão (em grego Πλάτων) nasceu um ano após a morte do estadista ateniense Péricles. Seu pai tinha como ancestral o rei Codros e sua mãe tinha Sólon entre seus antepassados. Inicialmente, Platão entusiasmou-se com a filosofia de Crátilo, um seguidor de Heráclito. No entanto, por volta dos 20 anos, encontrou o filósofo Sócrates e tornou-se seu discípulo até a morte deste. Pouco depois de 399 a.C., Platão esteve em Mégara com alguns outros discípulos de Sócrates, hospedando-se na casa de Euclides. Em 388 a.C., quando já contava quarenta anos, Platão viajou para a Magna Grécia com o intuito de conhecer mais de perto comunidades pitagóricas. Nesta ocasião, veio a conhecer Arquitas de Tarento. Ainda durante essa viagem, Dionísio I convidou Platão para ir a Siracusa, na Sicília. Platão parte para Siracusa com a esperança de lá implantar seus ideais políticos. No entanto, acabou por se desentender com o tirano local e retorna para Atenas. Em seu retorno, funda a Academia. A instituição logo adquire prestígio e a ela acorriam inúmeros jovens em busca de instrução e até mesmo homens ilustres a fim de debater ideias. Em 367 a.C., Dionísio I morre e Platão retorna a Siracusa a fim de uma vez mais tentar implementar suas ideias políticas na corte de Dionísio II. No entanto, o desejo do filósofo foi novamente frustrado. Em 361 a.C. volta pela última vez a Siracusa com o mesmo objectivo e pela terceira vez fracassa. De volta a Atenas em 360 a.C., Platão permaneceu na direcção da Academia até sua morte, em 347 a.C. [editar] Pensamento platônico
Em linhas gerais, Platão desenvolveu a noção de que o homem está em contato permanente com dois tipos de realidade: a inteligível e a sensível. A primeira, é a realidade, mais concreta, permanente, imutável, igual a si mesma. A segunda são todas as coisas que nos afetam os sentidos, são realidades dependentes, mutáveis e são imagens das realidades inteligíveis. Tal concepção de Platão também é conhecida por Teoria das Idéias ou Teoria das Formas. Foi desenvolvida como hipótese no diálogo Fédon e constitui uma maneira de garantir a possibilidade do conhecimento e fornecer uma inteligibilidade relativa aos fenômenos. Para Platão, o mundo concreto percebido pelos sentidos é uma pálida reprodução do mundo das Idéias. Cada objeto concreto que existe participa, junto com todos os outros objetos de sua categoria, de uma Idéia perfeita. Uma determinada caneta, por exemplo, terá determinados atributos (cor, formato, tamanho, etc). Outra caneta terá outros atributos, sendo ela também uma caneta, tanto quanto a outra. Aquilo que faz com que as duas sejam canetas é, para Platão, a Idéia de Caneta, perfeita, que esgota todas as possibilidades de ser caneta. A ontologia de Platão diz, então, que algo é na medida em que participa da Idéia desse objeto. No caso da caneta é irrelevante, mas o foco de Platão são coisas como o ser humano, o bem ou a justiça, por exemplo. O problema que Platão propõe-se a resolver é a tensão entre Heráclito e Parmênides: para o primeiro, o ser é a mudança, tudo está em constante movimento e é uma ilusão a estaticidade, ou a permanência de qualquer coisa; para o segundo, o movimento é que é uma ilusão, pois algo que é não pode deixar de ser e algo que não é não pode ser, assim, não há mudança. Ou seja (por exemplo), o que faz com que determinada árvore seja ela mesma desde o estágio de semente até morrer, e o que faz com que ela seja tão árvore quanto outra de outra espécie, com características tão diferentes? Há aqui uma mudança, tanto da árvore em relação a si mesma (com o passar do tempo ela cresce) quanto da árvore em relação a outra. Para Heráclito, a árvore está sempre mudando e nunca é a mesma, e para Parmênides, ela nunca muda, é sempre a mesma e é uma ilusão sua mudança. Platão resolve esse problema com sua Teoria das Idéias. O que há de permanente em um objeto é a Idéia, mais precisamente, a participação desse objeto na sua Idéia correspondente. E a mudança ocorre porque esse objeto não é uma Idéia, mas uma incompleta representação da Idéia desse objeto. No exemplo da árvore, o que faz com que ela seja ela mesma e seja uma árvore (e não outra coisa), a despeito de sua diferença daquilo que era quando mais jovem e de outras árvores de outras espécies (e mesmo das árvores da mesma espécie) é sua participação na Idéia de Árvore; e sua mudança deve-se ao fato de ser uma pálida representação da Idéia de Árvore. Platão também elaborou uma teoria gnosiológica, ou seja, uma teoria que explica como se pode conhecer as coisas, ou ainda, uma teoria do conhecimento. Segundo ele, ao vermos um objeto repetidas vezes, uma pessoa lembra-se, aos poucos, da Idéia daquele objeto, que viu no mundo das Idéias. Para explicar como se dá isso, Platão recorre a um mito (ou uma metáfora) que diz que, antes de nascer, a alma de cada pessoa vivia em uma Estrela, onde localizam-se as Idéias. Quando uma pessoa nasce, sua alma é "jogada" para a Terra, e o impacto que ocorre faz com que esqueça o que viu na Estrela. Mas ao ver um objeto aparecer de diferentes formas (como as diferentes árvores que se pode ver), a alma recorda-se da Idéia daquele objeto que foi vista na Estrela. Tal recordação, em Platão, chama-se anamnesis. [editar] A reminiscência Uma das condições para a indagação ou investigação acerca das Idéias é que não estamos em estado de completa ignorância sobre elas. Do contrário, não teríamos nem desejo nem poder de procurá-las. Em vista disso, é uma condição necessária (para tal investigação) que tenhamos em nossa alma alguma espécie de conhecimento ou lembrança de nosso contato com as Idéias (contato esse ocorrido antes do nosso próprio nascimento) e nos recordamos das Idéias por vê-las reproduzidas palidamente nas coisas. Deste modo, toda a ciência platônica é uma reminiscência. A investigação das Idéias supõe que as almas preexistiram em uma região divina onde contemplavam as Idéias. Podemos tomar como exemplo o Mito da Parelha Alada, localizado no diálogo Fedro, de Platão. Neste diálogo, Platão compara a raça humana a carros alados. Tudo o que fazemos de bom, dá forças às nossas asas. Tudo o que fazemos de errado, tira força das nossas asas. Ao longo do tempo fizemos tantas coisas erradas que nossas asas perderam as forças e, sem elas para nos sustentarmos, caímos no Mundo Sensível, onde vivemos até hoje. A partir deste momento, fomos condenados a vermos apenas as sombras do Mundo das Idéias. [editar] Conhecimento Platão não buscava as verdadeiras essências da forma física como buscavam Demócrito e seus seguidores, sob influência de Sócrates buscava a verdade essencial das coisas. Platão não poderia buscar a essência do conhecimento nas coisas, pois estas são corruptíveis, ou seja, variam, mudam, surgem e se vão. Como o filósofo deveria buscar a verdade plena, deveria buscá-la em algo estável, as verdadeiras causas, pois logicamente a verdade não pode variar, se há uma verdade essencial para os homens esta verdade dever valer para todas as pessoas. Logo, a verdade deve ser buscada em algo superior. Nas coisas devem ter um outro fundamento, que seja além do físico (metafísico), a forma de buscar estas realidades vem do conhecimento, não das coisas, mas do além das coisas. Esta busca racional é contemplativa, isto significa buscar a verdade no interior do próprio homem. Porém o próprio homem não é meramente sujeito particular, mas como um participante das verdades essenciais do ser. Platão assim como seu mestre Sócrates busca descobrir as verdades essenciais das coisas. O conhecimento era assim o conhecimento do próprio homem, mas sempre ressaltando o homem não enquanto corpo, mas enquanto alma. O conhecimento que continha na alma era a essência daquilo que existia no mundo sensível, assim em Platão também a técnica e o mundo sensível eram secundários. A alma humana enquanto perfeita participa do mundo perfeito das idéias, porém este formalismo só é reconhecível na experiência sensível. Também o conhecimento tinha fins morais, isto é, levar o homem à bondade e à felicidade. Assim a forma de conhecimento era um reconhecimento, que faria o homem dar-se conta das verdades que sempre já possuía e que o levavam a discernir melhor dentre as aparências de verdades e as verdades. A obtenção do autoconhecimento era um caminho árduo e metódico. Referente ao mundo material o homem pode ter somente a doxa (opinião) e téchne (técnica), que permitia a sobrevivência do homem, ao passo que referente ao mundo das idéias, ou verdadeiro conhecimento filosófico, o homem pode ter a épisthéme (verdadeiro conhecimento). Platão não defendia que todas as pessoas tivessem iguais acessos à razão. Apesar de todos terem a alma perfeita, nem todos chegavam à contemplação absoluta do mundo das idéias. [editar] Política "... os males não cessarão para os humanos antes que a raça dos puros e autênticos filósofos chegue ao poder, ou antes, que os chefes das cidades, por uma divina graça, ponham-se a filosofar verdadeiramente". (Platão). Esta afirmação de Platão deve ser compreendida baseado na teoria do conhecimento, e lembrando que o conhecimento para Platão tem fins morais. Mas cumpre ressaltar outro aspecto: Platão acreditava que existiam três espécies de virtudes baseadas na alma. A primeira virtude era a da sabedoria, deveria ser a cabeça do Estado, ou seja, a governante, pois possui caráter de ouro e utiliza a razão. A segunda espécie de virtude é a coragem, deveria ser o peito do estado, isto é, os soldados, pois sua alma de prata é imbuída de vontade. E, por fim, a virtude da temperança, que deveria ser o baixo-ventre do estado, ou os trabalhadores, pois sua alma de bronze orienta-se pelo desejo das coisas sensíveis. [editar] O Homem O homem para Platão era dividido em corpo e alma. O corpo era a matéria e a alma era o imaterial e o divino que o homem possuía. Ao passo que o corpo sempre está em constante mudança de aparência, forma... A alma não muda nunca, a partir do momento em que nascemos temos a alma perfeita, porém não sabemos. As verdades essenciais estão escritas na alma eternamente, porém ao nascermos esquecemos, pois a alma é aprisionada no corpo. A alma é divida em 3 partes: 1=> raciona: região da cabeça; esta tem que controlar as outras 2 partes 2=> torax: irascível; parte dos sentimentos. 3=> abdômen: concupiscível; desejo, mesmo carnal(sexual), ligado ao libido. Platão acreditava que a alma depois da morte reencarnava em outro corpo, mas a alma que se ocupava com a filosofia e com Bem esta era privilegiada ao morrer, a ela era concedida o privilégio de passar o resto de seus tempos em companhia dos deuses. O conhecimento da alma é que dá sentido à vida. Tudo foi criado pelo Demiurgo (seu criador), um divino artesão que criou o mundo real e sua aparência. Ação do homem se restringe ao mundo material, no mundo das idéias o homem não pode transformar nada. Porque se é perfeito não pode ser mais perfeito. [editar] Obra
Platão escreveu, principalmente, na forma de diálogos. A coleção desses escritos, considerados autênticos, e numa ordem provavelmente cronológica, são: 1. Hípias (menor): trata do agir humano; 2. Alcibíades (Primeiro): trata da doutrina socrática do auto-conhecimento; 1. Alcibíades (Segundo): trata do conhecimento; 3. Apologia de Sócrates: relata o discurso de defesa de Sócrates no tribunal de Atenas; 4. Eutífron: trata dos conceitos de piedade e impiedade; 5. Críton: trata da justiça; 6. Hípias (maior): discussão estética; 7. Laques: trata da coragem; 8. Lísis: trata da amizade/amor; 9. Cármides: diálogo ético; 10. Protágoras: trata do conceito e natureza da virtude; 11. Górgias: trata do verdadeiro filósofo em oposição aos sofistas; 13. Mênon: trata do ensino da virtude; 14. Fédon: relata o julgamento e morte de Sócrates e trata da imortalidade da alma; 15. Banquete: trata da origem, as diferentes manifestações e o significado do amor sensual; 16. Fedro: trata da retórica e do amor sensual; 17. Íon: trata de poesia; 18. Menêxeno: elogio da morte no campo de batalha; 19. Eutidemo: crítica aos sofistas; 20. Crátilo: trata da natureza dos nomes; 21. A República: aborda vários temas, mas todos subordinados à questão central da justiça; 22. Parmênides: trata da ontologia. É neste diálogo que o jovem Sócrates, a personagem, defende a teoria das formas que é duramente criticada por Parmênides; 23. Teeteto: trata exclusivamente da Teoria do Conhecimento; 24. Sofista: diálogo de caráter ontológico, discute o problema da imagem, do falso e do não-ser; 25. Político: trata do perfil do homem político; 26. Filebo: versa sobre o bom e o belo e como o homem pode viver melhor; 27. Timeu: trata da origem do universo. 28. Crítias: Platão narra aqui mito de Atlântida através de Crítias (seu avô). É um diálogo inacabado; 29. Leis: aborda vários temas da esfera política e jurídica. É o último (inacabado), mais longo e complexo diálogo de Platão; 30. Epidômite 31. Cartas (dentre as quais, somente a de número 7 é considerada relamente autêntica) Operações de transformação sobre sólidos [editar] Poliedros duais Dual cubo-octaedro O poliedro dual é obtido ligando os centros de todos os pares de faces adjacentes de qualquer sólido, produzindo-se outro sólido menor. [editar] Truncatura A Truncatura de um Sólido é uma operação que consiste em cortar os vértices ou as arestas de um sólido. [editar] Acumulação A Acumulação de sólidos é a operação dual da truncatura e consiste em substituir as faces poligonais por pirâmides. [editar] Snubificação A Snubificação de um Poliedro consiste em afastar as faces do poliedro, rodar as mesmas um certo ângulo (normalmente 45º) e preencher o espaço vazio entre as novas faces com triângulos. [editar] Expansão A Expansão de Sólido é um caso especial de uma Snubificação sem rotação. [editar] Composição Composição de Sólido consiste em colocar vários poliedros (ou sólidos) partilhando o mesmo centro. O poliedro resultante chama-se Poliedro composto. [editar] Estrelamento Estrelamento de um poliedro consiste em estender os planos definidos pelas suas faces até se intersectarem, formando assim um novo sólido. Um poliedro é regular quando todas as faces são polígonos regulares congruentes e todos os vértices são congruentes. Isto significa que existe uma simetria do poliedro que transforma cada face, cada aresta e cada vértice numa outra face, aresta ou vértice. É possível provar que existem apenas cinco poliedros regulares convexos. Os cinco poliedros regulares convexos — tetraedro, cubo ou hexaedro, octaedro, dodecaedro e icosaedro — ficaram conhecidos na história como sólidos platônicos, pelo fato de Platão ter construído suas teorias a respeito da origem do universo, associando a estes os constituintes fundamentais da natureza. Platão professava que Deus criou o mundo a partir de quatro elementos básicos: a terra, o fogo, o ar e a água. Ele procurou, então, definir as essências específicas desses elementos através de quatro objetos geométricos, os poliedros convexos regulares, que representavam, aos olhos dos gregos, harmonia e uma certa perfeição. . a terra, o elemento mais imóvel, Platão associou ao cubo, o único poliedro com faces quadradas, e dessa forma, o mais apto a garantir estabilidade; . o fogo ele atribuiu ao tetraedro, que é o poliedro mais "pontudo", com arestas mais cortantes, com menor número de faces e de maior mobilidade; . a água e o ar, que são de mobilidade crescente e intermediária entre a terra e o fogo, ele atribuiu respectivamente ao icosaedro e ao octaedro. Com o tempo, aparece o quinto e último poliedro regular convexo: o dodecaedro. Platão explicita suas idéias sobre o quinto elemento: o cosmos, que segundo ele seria a "alma do mundo". Outros Trabalhos Relacionados
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Platão de Atenas
(428/27 a.C. — 347 a.C.) foi um filósofo grego. Discípulo de Sócrates,
fundador da Academia e mestre de Aristóteles. Acredita-se que seu nome
verdadeiro tenha sido Aristócles; Platão era um apelido que,
provavelmente, fazia referência à sua caracteristica física, tal como o
porte atlético ou os ombros largos, ou ainda a sua ampla capacidade
intelectual de tratar de diferentes temas. Πλάτος (plátos), em grego
significa amplitude, dimensão, largura. Sua filosofia é de grande
importância e influência. Platão ocupou-se com vários temas, entre eles
ética, política, metafísica e teoria do conhecimento.
Detalhe de Platão, n'A
Escola de Atenas, obra do renascentista Rafael.
Platão ensina filosofia.
Mosaico romano de Pompéia