|
Introdução O grupo elaborou o trabalho com o objectivo de conhecer melhor quem foi Pitágoras e os bens que trouxe para o desenvolvimento da Matemática. Como gostaríamos de entender a maneira como se aplica o seu teorema, expomos seguidamente algumas das suas demonstrações. Biografia de Pitágoras
A sua vida está envolta em lendas, uma delas, é o facto de o seu nome significar “Altar da Pítia”, porque a sua mãe ao consultar Pitunisa (a mulher que se encontrava ao serviço de Deus e pronunciava os oráculos) soube que a criança iria ser uma pessoa ilustre. Pitágoras alcançou grandes feitos na sua vida, tais como: . Invenção do seu teorema (Teorema de Pitágoras); . Fundação da Escola Pitagórica; . Criação de algumas leis; . Criação da tábua de Pitágoras. O Teorema de Pitágoras diz: num triângulo rectângulo, o quadrado construído sobre a hipotenusa é igual à soma do quadrado construído sobre os catetos. Esta regra aplica-se a todos os triângulos rectângulos, tendo sido realizadas diversas demonstrações para o provar.
O seu Teorema é usado hoje na construção de telhados triangulares para as casas, calculando as medidas que as vigas devem ter, respeitando a inclinação e outros factores como, por exemplo, o tipo de telha. A partir daí, começaram a construir-se templos perfeitos e perpendiculares ao chão.
A Escola Pitagórica foi
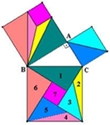
fundada no sul de Itália em Crotona, . Os números absolutos ou a Aritmética; . Os números aplicados ou a Música; . As grandezas no estado de repouso ou a geometria; . As grandezas em movimento ou a Astronomia. A tábua de Pitágoras é o que hoje em dia se conhece como tabuada ou tábua de multiplicações. Foi inventada pelos pitagóricos e é aplicada para qualquer multiplicação. Pitágoras realizou também diversas viagens ao longo da sua vida: . A Crotona, em Itália, onde fundou a Escola Pitagórica e onde se fixou aos 35 anos. . Ao Egipto e à Babilónia, onde entrou em contacto com Matemáticos da época; . À Pérsia e a Creta. Faleceu em 497 a.C., com 83 anos, em Metaponto, deixando para trás feitos importantes e indispensáveis à disciplina de Matemática. Demonstrações do Teorema de Pitágoras Na altura, várias pessoas ligadas à sabedoria da época puseram em causa esse teorema e se realmente se aplicava a todos os triângulos rectângulos. Então, os Pitagóricos e Pitágoras, procederam a várias demonstrações para comprovar a sua teoria. Seguidamente, expomos algumas dessas demonstrações. A seguinte demonstração foi a que Pitágoras usou para comprovar a sua teoria. Um possível problema para estas figuras seria calcular a área dos quadrados a verde.
(As medidas expostas no quadrado1 são as mesmas para o quadrado2) Os triângulos azuis são geometricamente iguais. Os quadrados 1 e 2 são geometricamente iguais. Se os triângulos são geometricamente iguais, o quadrado a verde da figura 1 tem a mesma área que os quadrados da figura 2, logo: A2+A1óa2 + b2 + 4T= c2 +4tóa2+b2=c2 Para melhor entender as diferentes maneiras de demonstrar o teorema de Pitágoras, expomos, seguidamente, outro exemplo.
Como dá, através da mesma, para comprovar, a soma do quadrado dos catetos é igual ao quadrado da hipotenusa.
A imagem é apenas um
exemplo, porque consegue-se decompor o quadrado em mais figuras e obter
o mesmo resultado. A imagem representa outra possível decomposição dos “quadrados” do triângulo. Neste caso decompusemos os catetos em mais figuras. Conclusão O grupo concluiu que: Pitágoras foi um grande filósofo e matemático grego da Antiguidade. Sem ele, não se teria descoberto inúmeras coisas. Em especial a tabuada, que é indispensável nos dias de hoje. Entendemos melhor a maneira como ele provou a sua teoria. Ficámos a saber, também, que a Matemática depois de compreendida, em alguns casos, é bastante simples. Bibliografia www.wikipédia.com www.educ.fc.ul.pt www.exatas.com www.penta.ufrgs.br www.potfoliomatematica.no.sapo.pt Outros Trabalhos Relacionados
|
|
 Pitágoras
foi um grande filósofo e matemático Grego do período Pré-socrático.
Nasceu numa ilha Grega chamada Samos, no mar Egeu, em 580 a.C.
Pitágoras
foi um grande filósofo e matemático Grego do período Pré-socrático.
Nasceu numa ilha Grega chamada Samos, no mar Egeu, em 580 a.C.
 Conta a
lenda que, como prova de gratidão por ter demonstrado esse teorema,
Pitágoras sacrificou 100 bois aos deuses.
Conta a
lenda que, como prova de gratidão por ter demonstrado esse teorema,
Pitágoras sacrificou 100 bois aos deuses. onde aqueles que lá aprendiam se chamavam Pitagóricos. O seu lema era “O
número é tudo”. Essa expressão significava que tudo no Universo era
regido pelos números e suas relações. Os Pitagóricos dividiam os
assuntos matemáticos em quatro secções:
onde aqueles que lá aprendiam se chamavam Pitagóricos. O seu lema era “O
número é tudo”. Essa expressão significava que tudo no Universo era
regido pelos números e suas relações. Os Pitagóricos dividiam os
assuntos matemáticos em quatro secções: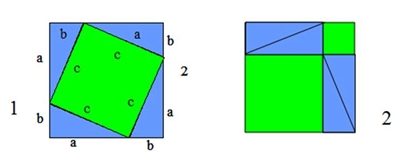
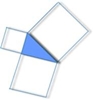
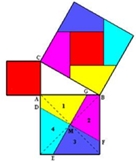 Para
provar que o teorema de Pitágoras se aplica a todos os triângulos
rectângulos, basta decompor o quadrado dos catetos em várias figuras e
tentar encaixá-las no quadrado da hipotenusa, como enuncia a figura.
Para
provar que o teorema de Pitágoras se aplica a todos os triângulos
rectângulos, basta decompor o quadrado dos catetos em várias figuras e
tentar encaixá-las no quadrado da hipotenusa, como enuncia a figura.